题目

#

给你一个二叉树的根结点 root，该二叉树由恰好 3 个结点组成：根结点、左子结点和右子结点。

如果根结点值等于两个子结点值之和，返回 true ，否则返回 false 。

示例1：

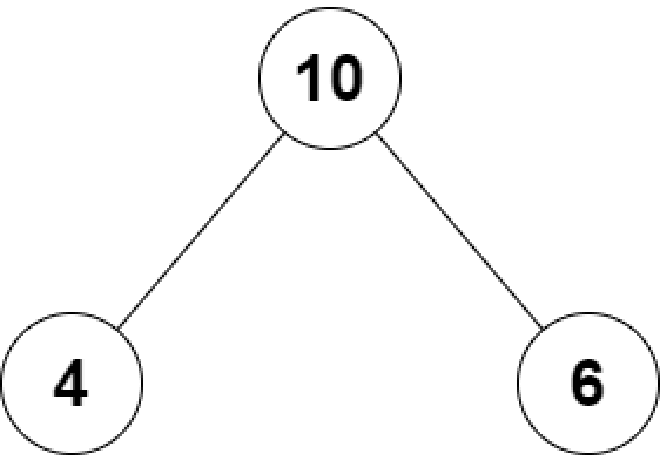
输入：root = [10,4,6]

输出：true

解释：根结点、左子结点和右子结点的值分别是 10 、4 和 6 。

由于 10 等于 4 + 6 ，因此返回 true 。

示例2：

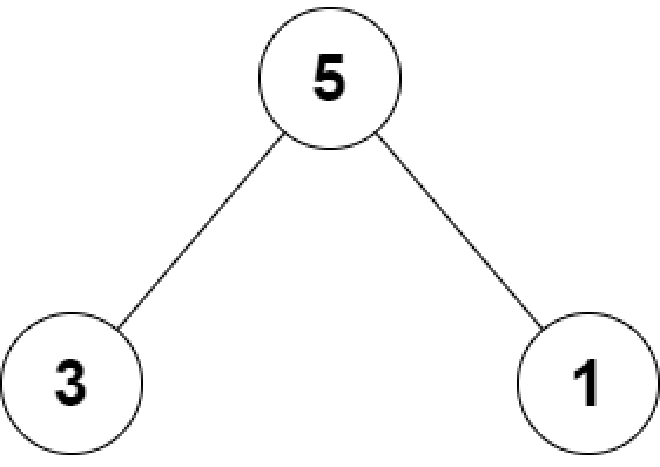
输入：root = [5,3,1]

输出：false

解释：根结点、左子结点和右子结点的值分别是 5 、3 和 1 。

由于 5 不等于 3 + 1 ，因此返回 false 。

题解

#

方法一：递归解法

#

思路

#

我们可以使用递归的方法来解决这个问题。首先，我们定义一个递归函数 is_sum_equal，该函数接受一个二叉树的根结点作为参数，并返回一个布尔值。

在递归函数中，我们首先检查根结点是否为空。如果为空，返回 false。然后，我们计算左子结点和右子结点的值之和，如果与根结点的值相等，则返回 true，否则返回 false。接下来，我们递归调用 is_sum_equal 函数来判断左子树和右子树是否满足条件。

这样，我们可以通过递归遍历整个二叉树，判断每个结点是否满足条件。如果任何一个结点满足条件，即根结点的值等于左子结点和右子结点的值之和，那么整个二叉树就满足条件，返回 true。否则，返回 false。

复杂度分析

#

• 时间复杂度：对于每个结点，我们遍历它一次，所以时间复杂度为 O(n)，其中 n 是二叉树中的结点数。
• 空间复杂度：递归调用的栈空间最大为二叉树的高度，最坏情况下为 O(n)，其中 n 是二叉树中的结点数。

实现

#

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkTree(TreeNode* root) {
        return is_sum_equal(root);
    }

    bool is_sum_equal(TreeNode* node) {
      if (!node) {
        return false;
      }

      if (!node->left || !node->right) {
        return false;
      }

      if ((node->left->val + node->right->val) == node->val) {
          return true;
      }

      return is_sum_equal(node->left) || is_sum_equal(node->right);
    }
};