Time, Clocks and the Ordering of Events in a Distributed System 这篇论文涉及到偏序和全序,因此特地理解了一下这些概念。
一些基本概念 #
- 自反性, 任取一个 $A$ 中的元素 $x$,如果都有 $\lbrace x,x \rbrace$ 在 $R$ 中,那么 $R$ 是自反的。
- 对称性, 任取$A$ 中的元素 $x,y$,如果 $\lbrace x,y \rbrace$ 在关系 $R$ 上, $\lbrace y,x \rbrace$ 也在关系 $R$ 上,那么 $R$ 是对称的。
- 反对称性, 任取一个 $A$ 中的元素 $x,y \land (x != y)$,如果$\lbrace x,y \rbrace$ 在关系 $R$ 上, 而 $\lbrace y,x \rbrace$ 不在关系$R$ 上,那么 $R$ 是反对称的。
- 传递性, 任取一个 $A$ 中的元素 $x,y,z$,如果 $\lbrace x,y \rbrace,\lbrace y,z \rbrace$ 在关系 $R$ 上,那么 $\lbrace x,z \rbrace$ 也在关系 $R$ 上,那么 $R$ 是对称的。
示例 #
假设 $A$ 是一个集合 $\lbrace 1,2,3 \rbrace;$ $R$ 是集合 $A$ 上的关系
$$ R = \lbrace <1,1>,<2,2>,<3,3>,<1,2>,<1,3>,<2,3> \rbrace $$
验证这些性质:
- 自反性:任取集合 $A = \lbrace 1,2,3 \rbrace$ 中的每个元素 $\lbrace x,x \rbrace$ 都有 $\lbrace (1,1),(2,2),(3,3) \rbrace;$ 是满足自反性的。
- 对称性:任取集合 $A = \lbrace 1,2,3 \rbrace$ 中的每个元素 $\lbrace x,y \rbrace$, 但是对于 $\lbrace 1,2 \rbrace$ 是找不到 $\lbrace 2,1 \rbrace$ 的,因此是不满足对称性的。
- 反对称性:根据反对称性的定义,集合 $A = \lbrace 1,2,3 \rbrace$ 中的每个元素 $\lbrace x,y \rbrace \land (x!=y)$ 在关系R上,而 $\lbrace y,x \rbrace$ 不在关系 $R$ 上。 例如 $\lbrace 1,2 \rbrace$ 找不到 $\lbrace 2,1 \rbrace$ ,$\lbrace 1,3 \rbrace$ 找不到 $\lbrace 2,1 \rbrace$ ,因此是满足反对称性的 。
- 传递性:根据传递性的定义,任取集合 $A = \lbrace 1,2,3 \rbrace$ 中的每个元素 $\lbrace x,y,z \rbrace$, 这里取 $\lbrace 1,2,3 \rbrace$, $\lbrace 1,2 \rbrace, \lbrace 2, 3 \rbrace$ 在关系 $R$ 上,$\lbrace 1, 3 \rbrace$ 也在关系 $R$ 上,因此 $R$ 是满足对称性的。
偏序 #
偏序可以理解为,满足自反性、反对称性、传递性,但不满足对称性,即对于集合 $A$ 的 $\lbrace x,y \rbrace$ 在关系 $R$ 上,且 $\lbrace y,x \rbrace$ 也在关系 $R$ 上。
全序 #
可以理解为全序也是一种偏序,但它和偏序是有区别的,关键区别在于反对称性上:
- 偏序性质下,A 中的 $\lbrace x,y \rbrace$ 在关系 $R$ 上, $\lbrace y,x \rbrace$ 不在关系 $R$ 上,那么就产生一个问题: $\lbrace y,x \rbrace$ 的关系是什么?也就是说,偏序情况下,集合 $A = \lbrace x,y,z,k \rbrace$ 总是存在一些元素的关系根据 $R$ 是无法得到的。
- 全序性质下,为偏序的性质增加了一个关键性的条件,让其满足 $\lbrace x\le y \rbrace \lor \lbrace y\le x \rbrace$,且二者只能存在一个,因此就能得知 $\lbrace y,x \rbrace$ 的关系是什么了!
偏序举例 #
假设有 $A=\lbrace 1,2,3,4 \rbrace$,假设 $R$ 是集合 $A$ 上的关系
$$ R = \lbrace \lbrace 1,1 \rbrace,\lbrace 2,2 \rbrace, \lbrace 3,3 \rbrace, \lbrace 4,4 \rbrace, \lbrace 1,2 \rbrace,\lbrace 1,4 \rbrace,\lbrace 2,4 \rbrace,\lbrace 3,4 \rbrace \rbrace $$
那么:
- 自反性, 可以看到 $\lbrace 1,1 \rbrace,\lbrace 2,2 \rbrace, \lbrace 3,3 \rbrace, \lbrace 4,4 \rbrace$ 都在R中,满足.
- 反对称性, 由于 $\lbrace 1,1 \rbrace,\lbrace 2,2 \rbrace, \lbrace 3,3 \rbrace, \lbrace 4,4 \rbrace$ 不属于 $x !=y$ ,所以不考虑这4种,对于 $\lbrace 1,2 \rbrace$,有 $\lbrace 2,1 \rbrace$ 不在 $R$ 中;对于$\lbrace 2,4 \rbrace$ 有 $\lbrace 4,2 \rbrace$不在 $R$ 中;对于$\lbrace 3,4 \rbrace$ 有$\lbrace 4,3 \rbrace$ 不在 $R$中,满足.
- 传递性, 满足.
- $\lbrace 1,1 \rbrace, \lbrace 1,2 \rbrace$在 $R$ 中,并且 $\lbrace 1,2 \rbrace$ 在 $R$ 中;
- $\lbrace 1,1 \rbrace, \lbrace 1,4 \rbrace$在 $R$ 中,并且 $\lbrace 1,4 \rbrace$ 在 $R$ 中;
- $\lbrace 2,2 \rbrace, \lbrace 2,4 \rbrace$在 $R$ 中,并且 $\lbrace 2,4 \rbrace$ 在 $R$ 中;
- $\lbrace 3,3 \rbrace, \lbrace 3,4 \rbrace$在 $R$ 中,并且 $\lbrace 3,4 \rbrace$ 在 $R$ 中;
全序举例 #
假设有 $A=\lbrace a,b,c \rbrace$,假设 $R$ 是集合 $A$ 上的关系
$$ \lbrace \lbrace a,a \rbrace,\lbrace b,b \rbrace,\lbrace c,c \rbrace,\lbrace a,b \rbrace,\lbrace a,c \rbrace,\lbrace b,c \rbrace \rbrace $$
和偏序上述一样,可以证明具有自反性,反对称性,传递性,所以是偏序的。
又因为有 $\lbrace a,b \rbrace,\lbrace a,c \rbrace,\lbrace b,c \rbrace$, 也就是说两两关系都有了,所以满足对于任意的 $A$ 集合上的 $x,y$,都有 $x \le y$,或者 $y \le x$,且二者只存在一种情况,所以是全序的。
概念在论文中的作用 #
在 《Time, Clocks, and the Ordering of Events in a Distributed System》 论文中,偏序和全序主要用来定义一个事情是在另一个事情之前发生。
在单机环境下,这个关系很好定义。但在分布式系统中,假设有A,B两个服务器,他们的本机时间可能不同步的,或者有差别的,或者说不准的,那么这个时候,很难定义A服务器的这个请求先发生,还是B服务器的这个请求先发生。
所以在论文里面,Lamport 是这样定义的:
- If a and b are events in the same process, and a comes before b, then $a \to b$.
- if a is the sending of a message by one process and b is the receipt of the same message by another process, then $a \to b.$
- If $a \to b$ and $b \to c$ then $a \to c$. Two distinct events a and b are said to be concurrent if $\lnot(a \to b)$ and $\lnot(b \to a)$.
Two distinct events a and b are said to be concurrent if $\lnot(a \to b)$ and $\lnot(b \to a)$.
这一段其实定义了全序,若是没有这一段定义,我们看一下会发生什么。
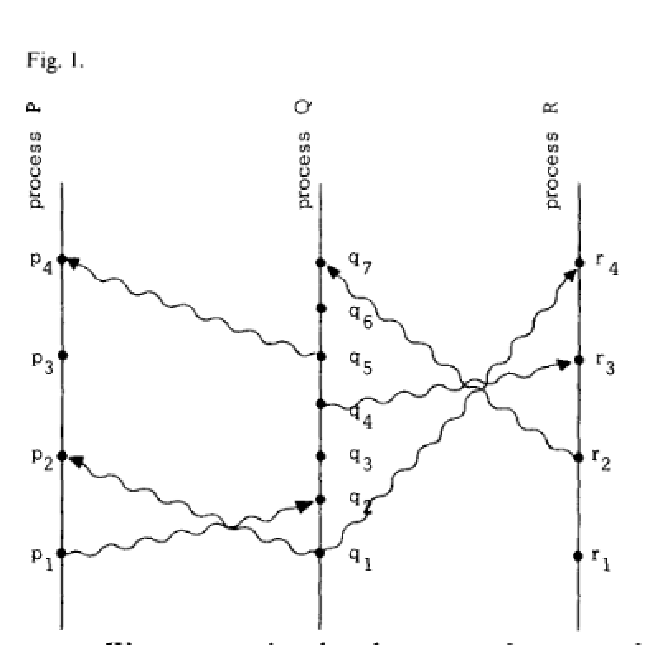
下图可以看到 3 个服务
- P 服务在 p3 处理一个请求,Q 服务在 q3 也处理一个请求,并且这两个请求没有任何关系,那么他们谁先谁后?换句话说,如何定义 p3 和 q3 的顺序?
- 从图中看起来是 q3 先,但是 P 服务 在 p4 节点之前根本不知道 Q 服务的 q3 实际的运行时间是什么。
所以这个时候,Lamport 认为这种情况下这两个事件p3和q3算是并发的。
那么如何解决这个问题呢?这里简单的说一下,因为论文思路不是本文重点。
分布式系统中很难获知全局的全序关系,论文中提出一种方法,可以基于 Happened Before 这种偏序关系。(因果一致性),扩展出强一致性的全序关系。
论文中以此关系建立了逻辑时钟(Lamport Scalar Clock),用于确立 Happened Before 偏序关系:
$Clock \space Condition. \space For \space any \space events \space a, b:$
$$ if \space a\to b \space then \space C(a) < C(b) $$
也就是说通过定义 Happend Before 为偏序关系得到一个全序关系。
总结 #
- 偏序关系满足自反、反对称、传递的性质。在存在反对称性下,$\lbrace x,y \rbrace$ 和 $\lbrace y, x \rbrace$ 只有一个在关系上, 因此关系 $R$ 中的一些关系是无法确定发生顺序的。
- 全序关系为偏序关系加入了约束条件。在分布式系统下,全局全序关系很难得知,论文通过 Happend Before 为偏序关系扩展出强一致性的全序关系。
