首先,简要回顾一下。
上一篇文章我们将零知识证明定义为两个计算机程序(或图灵机)之间的相互作用,互动双方分别称为证明者和验证者,证明者试图说服验证者某些数学陈述是真实的。 我们还介绍了一个具体的例子:Goldreich,Micali和Wigderson 提出的一个很有意思的协议, 平面图三色问题的零知识证明。
在上一篇中我们描述了任何零知识证明都必须满足的三个关键属性:
- 完备性(completeness): 如果证明者是诚实的,那么她最终会说服验证者。
- 可靠性(Soundness): 证明者只能说服验证者该陈述是否属实。
- 零知识性(Zero-knowledgeness): 除了知道陈述是真实的,验证者不知道任何额外的信息。
真正的挑战来自如何定义最后一个属性。 你如何判断验证者无法获取除了陈述之外的任何信息呢?
如果您没有读过前一篇文章,我可以告诉你一个由 Goldwasser,Micali和Rackoff 三人提出一个非常赞的方案。 他们认为一个协议如果满足对于每一个可能的验证者,可以证明一个叫“模拟器”的算法的存在,并且这个算法有一些非常特殊的属性,就认为它满足零知识证明 。
机械地来看,模拟器就像一个特殊的证明者。 不过与真正的证明者不同,后者以一些能够证明陈述真实性的特定信息开始, 模拟器则不会 [作者注1]。然而模拟器必须能够“欺骗”每一个验证者使他们相信该陈述是真实的,同时产生与真实证明者在统计意义学上相同(或者说无法区分)的输出结果副本。
逻辑流程非常清晰:由于模拟器没有“知识”能被提取,因此显然验证者在与之交互后无法获得任何有价值的信息。 此外,如果交互的信息副本与使用正常证明者运行的真实协议的分布相同,那么验证者对于真正的证明者的验证结果不会比对于模拟器的验证结果更精确。 (如果更精确,那么这意味着模拟器与真正的证明者的分布在统计学上是不相同的。)因此,验证者无法从真实的协议运行中提取有用的信息。
这令人难以置信,更糟的是,这似乎还是矛盾的! 我们要求一个协议是完全可靠的,这意味着一个伪造的证明者除非具备特定的信息证明某个陈述的真实性,否则他无法欺骗验证者接受,但是我们也要求存在一个算法 (模拟器),可以从字面上作弊。 显然这两个属性不能同时存在。
解决方案是这两个属性(可靠性和“可作弊”的算法)不 同时存在。
为了构建模拟器,我们可以对验证者执行那些在现实世界中永远不可能做到的事情。 前一篇文章中给出的例子是使用“时光机”。也就是说,“模拟器”可以回滚验证者程序的执行,以达到’欺骗’它的目的。 因此,在这个可以倒转验证者时间的世界里,很容易证明模拟器的存在。 而在现实世界中当然不可能做到。 这个“伎俩”使我们绕开了上面所说的矛盾。
最后提醒下,为了说明所有这些想法,我们介绍了一个由 Goldreich,Micali和Wigderson(GMW)设计的通用零知识证明。该协议使我们能够以零知识证明某张图符合三色问题。当然,三色问题的零知识证明并不是非常有趣。 GMW结果的真正意义是理论上的。由于已知三染色问题属于NP完全问题,所以GMW协议可用于证明 NP问题中的任何陈述。 这是相当厉害的。
我来稍微详细地解释下:
- 如果存在可以在多项式时间内验证证人(解决方案)的任何 决策问题(即可以用是/否回答的问题),则:
- 我们可以通过(1)将问题转化为三色问题的一个实例,以及(2)运行 GMW 协议来证明 [作者注1]。
这个令人兴奋的结果使我们能够交互式零知识证明NP问题中的每个陈述。唯一的问题是它几乎无法使用。
理论付诸实践 #
如果你是一个实践主义者,那么你可能不会认同这个零知识证明。因为实际上使用这个方法 的代价非常昂贵并且很愚蠢。很可能你会将问题以布尔电路来表示,当且仅当有正确的输入,电路输出结果就为真。然后你又得把电路翻译成图表,导致工作量爆炸式增加。 最后你还需要运行成本很高的 GMW 协议。
所以实际上没有人会这样做。 这被认为是“可行性”结果。 一旦你认为某个事情有可行性,下一步就是提高效率。
其实我们几乎每天都会使用零知识证明。 在这篇文章中,我将花一些时间来讨论更具实际意义的零知识证明。 不过我需要做一些背景介绍。
证明vs知识证明 #
深入讨论之前,还有一个概念需要确认。 具体来说,我们需要讨论当我们实施零知识证明时,我们在证明什么。
我解释下。 概括地讲,可能有两类陈述需要用零知识证明。 粗略地说,分成如下几部分。
有关“事实”的陈述。 例如,我可能希望证明“一个特定的图可以进行三染色”或“数字N是一个合数”。 这些都是关于内在属性的陈述。
关于我个人知识的陈述。 此外,我可能希望证明我知道某些信息。这类陈述的例子有:“我知道这个图的三染色方案”,或者“我知道N的因式分解”。这不仅仅证明某个情况是真实的,而且实际上依赖于证明者所知道的信息。
认识到这两种陈述之间存在巨大差异是很重要的!例如,即使你不知道完整的因式分解,也可能证明数字 N 是合数。因此,仅仅证明第一个陈述并不等于同时证明了第二个陈述。
第二类证据被称为“知识证明”。这对证明我们在现实生活中使用的各种陈述非常有用。本篇我们将主要关注它。
Schnorr 身份识别协议 #
我们已经介绍了一些必要的背景知识,现在我们继续来看看 Claus-Peter Schnorr 在20世纪80年代发明一个的特定的并且非常有用的知识证明。Schnorr 协议乍一看有些奇怪,但实际上它是我们现代许多签名方案的基础。
然而,Schnorr 关注的并不是数字签名,而是身份识别。具体来说,我们假设 Alice 已经将公钥对外发布,然后想要证明她拥有与该公钥对应的私钥。这是我们在真实世界的协议中遇到的很确切问题,例如 SSH 公钥,所以它的意义还是存在的。
Schnorr首先假设公钥有一种非常具体的格式。具体来说,令 p 为素数,令 g 为素数 q 的循环群的生成元。 为了生成密钥对,Alice 首先选择 1到q 之间的随机整数 a,然后计算密钥对:
$$ SK_A = a $$
(如果你对公钥加密比较了解,可能会注意到这是用于 Diffie-Hellman 和 DSA签名 算法的相同类型的密钥。这不是巧合,它对这个协议意义很大。)
Alice将自己的私钥保留,但她可以随意对外发布公钥。当她想证明她的私钥加密的信息时,她与Bob进行以下的交互协议:
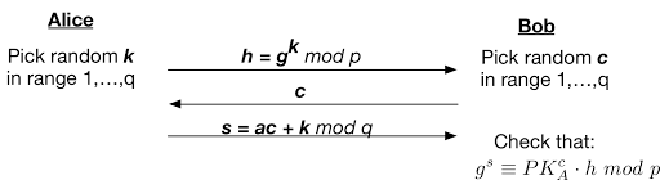
这里面涉及的知识点很多,所以我们花点时间剖析一下。
首先,我们应该问自己协议是否完整。这通常是最简单的可以验证的属性:如果Alice诚实地执行协议,Bob是否应该对结果满意? 在这种情况下,通过进行一些代入替换就可以很容易地看到完整性:
$$ \begin{alignat*}{2} g^s &\equiv PK^c_A \space \cdot \space h\space mod \space p\\ g^{ac+k} &\equiv (g^a)^c \space \cdot \space g^k\space mod \space p\\ g^{ac+k} &\equiv g^{ac+k}\space mod \space p\\ \end{alignat*} $$
可靠性证明 #
比较难证明的属性是可靠性。主要是因为对于知识证明的可靠性还没有很好的定义。请记住,这里(可靠性)我们想要说明的是:
如果Alice可以让Bob信服,那么她必定知道私钥 a .
看看上面的方程很容易理解,Alice欺骗协议的唯一方法是知道私钥a。但这并不能作为问题的证明。
当谈到知识证明的可靠性时,有一个非常好的方法。就像我们上面讨论的模拟器一样,我们需要证明一个特定算法的存在。这种算法被称为“信息提取器 ”,就是它字面的意思。信息提取器(或简称为“提取器”)是一种特殊类型的验证者,与证明者交互。并且如果证明者成功完成了证明,提取器应该能够提取证明者的私钥。
这回答了上面的问题。为证明知识证明的可靠性,我们必须表明对应每个可能的证明者都存在一个提取器。
当然,这与零知识协议似乎是矛盾的, 我们不应该能够从证明者那里获取私钥。
幸运的是,我们已经用“模拟器”解决了这个难题。 我们采取同样的方法:在正常协议运行期间,提取器不需要开启。如果我们允许随意回退证明者,就可以直接让提取器开始运作了。在这种情况下,我们将使用“倒带”来回退证明者的执行并提取私钥。
Schnorr 协议的提取器非常聪明,也非常简单。我们用协议交互图来说明它。 Alice(证明者)在左边,提取器在右边:
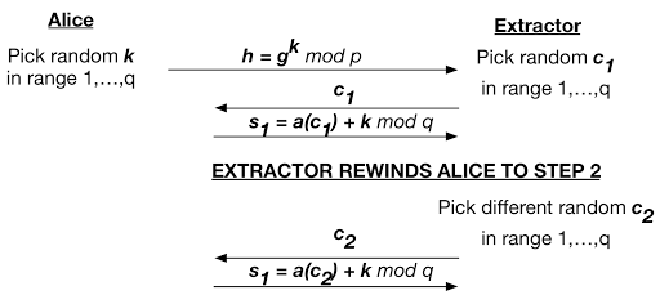
这里的关键点是,通过回退Alice的执行,提取器可以“欺骗”Alice使用相同的 k 来制作两个不同的证明副本。 这通常不会发生在真正的协议运行中,因为Alice每次执行协议都会使用新的 k。
如果提取器可以欺骗Alice做这件事,那么他可以通过下面的简单方程式来获取Alice的私钥:
$$ \begin{alignat*}{2} & (s_1 - s_2)/(c_1 - c_2)\mod q \\ &= (ac_1 + k) - (ac_2 + k) / (c_1 - c_2)\mod q \\ &= a(c_1 - c_2) / (c_1 - c_2)\mod q \\ &= a \end{alignat*} $$
这需要引起我们的注意了,因为这引出了 Schnorr 协议中的严重漏洞。 如果你不小心在协议的两次不同运行中使用相同的 k,攻击者就可能获取您的私钥! 如果你用了一个有问题的随机数发生器,这很可能会发生。
事实上经验丰富的人会注意到,这类似于这一次对 ECDSA 或 DSA 签名的系统(带有有问题的随机数发生器)的攻击! 而且这也不是巧合。 (EC)DSA 签名机制本来就是基于Schnorr 协议。 讽刺的是,DSA 的开发者设法保留了 Schorr 协议家族的这个弱点,同时 又放弃了让 Schnorr 协议如此好用的安全性证明。
对一个诚实的验证者证明零知识 #
现在我们证明完 Schnorr 签名是完整和可靠的,还需证明其是“零知识”的。 还记得吗?要证明零知识性,通常我们需要一个模拟器来完成,它可以与任何可能的验证者进行交互,并生成一个证明的结果“模拟”副本,即使模拟器不知道对应的私钥,也要证明它是知道的。
标准 Schnorr 协议中并没有这样的模拟器,马上我就会解释原因。相反,为了让证明顺利开展,我们需要做一个特定的假设。这就是:验证者需要“诚实”。也就是说,我们需要假设,验证者会正确运行协议里它要证明的部分,也就是说,它将仅使用随机数生成器来挑选它的尝试值 “c”,并且不会基于任何我们提供的输入来挑选这个值 。只要保证这一点,我们就可以开始构建模拟器了。
模拟器的工作方式是这样的。
假设我们试图证明我们知道某个公钥 $g^a \mod p$ 的私钥 $a$,但是我们实际并不知道 $a$ 的值。 模拟器假设验证者会选择某个 $c$ 值来尝试,而且前提是诚实的验证者只会根据它的随机数发生器来选择数值 c,而不是基于证明者的任何输入。
- 首先输出初始信息 $g^{k_1}$ 作为证明者的第一条消息,并找出验证者选择的尝试值 $c$。
- 回退验证者(验证器),并在 ${0,…q-1}$ 范围内选取一个随机整数 $z$。
- 计算 $g^{k_2} = g^z * g^{a(-c)}$ 并输出 $g^{k_2}$ 为证明者的新初始消息。
- 验证者再次尝试 $c$ 时,输出值 $z$ 。
请注意,副本 $g^k,c,z$ 将被视为对 $a$ 值有效且分布均匀的知识证明。 验证者会接受这个输出作为对 $a$ 值有效的知识证明,哪怕模拟器一开始并不知道私钥 $a$ !
这证明了如果我们可以回退验证者(器) ,那么(正如在本系列的第一篇文章中一样),我们总能“欺骗”验证者相信我们掌握了某个值的信息,哪怕在我们其实并不知道。 由于我们协议的统计分布与真实协议相同,意味着协议对一个诚实的验证者而言必然是零知识。
从交互到 非交互 到目前为止,我们已经解释类如何使用 Schnorr 协议来交互地证明与公钥 $g^a$ 对应的私钥 $a$ 的信息。 这是一个非常有用的协议,但只有验证者在线并愿意与我们交互时才有效。
一个容易想到的问题是我们是否可以在非交互的情况下使用该协议。具体而言,你不在线的情况下,我可以完成证明吗。这种证明被称为 非交互式零知识证明(NIZK)。将 Schnorr 协议转化为非交互式证明看起来是相当困难的,因为该协议从根本上依赖于验证者随机的尝试。不过好在我们可以使用一个聪明的技巧。
这项技术是 Fiat 和 Shamir 在20世纪80年代开发的。 他们发现,如果你有一个靠谱的散列函数,你可以通过使用散列函数挑选尝试值来将交互式协议转换为非交互式协议。
具体而言,证明公钥 $g^a$ 对应的私钥a的改进后的知识证明协议如下:
- 证明者选择 $g^k$ (就像在交互协议中那样)。
- 现在,证明者计算一个尝试值 $c = H(g^k || M)$ 其中 $H()$ 是散列函数,并且M是(可选的)任意的消息字符串。
- 计算 $ac + k \mod q$ (就像在交互协议中那样)。
这里的结果是散列函数在没有和验证者交互的情况下挑选出了尝试值 $c$。原则上,如果散列函数“足够强”(意思是它是一个随机预言器),那么结果是证明者在非交互的情况下完成了 $a$ 的知识证明,可以把结果发给验证者了。而且这种方式相对简单。
这个协议特别巧妙的是,它不仅仅是一个知识证明,也是一个签名机制。 也就是说,如果将消息放入(可选)值 $M$ 中,将获得一个只有拥有私钥 $a$ 的人能生成的签名。 由此产生的协议被称为 Schnorr 签名机制,它也是现实中像 EdDSA 这样密钥方案的基础。
注解 #
- 作者注1: 在这个定义中,陈述必须是真实的。
