这篇文章的灵感来自两篇伟大的论文,这两篇论文使广大读者能够获得零知识证明:
- [1] How to Explain Zero Knowledge Protocols to Your Children (Quisquater et. al.)
- [2] Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles (Gradwohl et. al.).
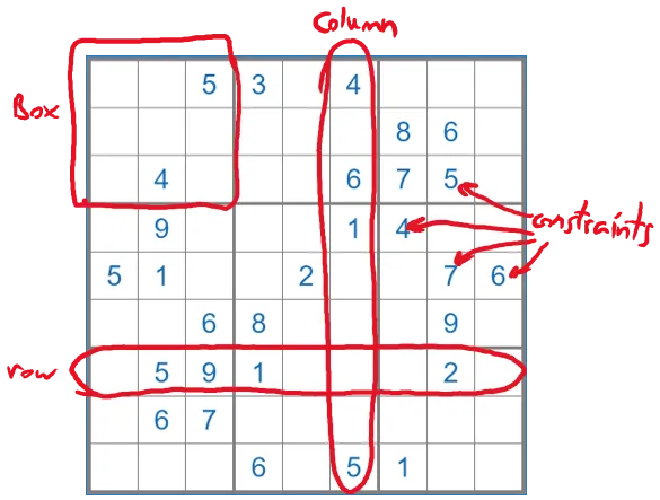
爱丽丝、鲍勃和查理喜欢解决数独问题。这三个朋友喜欢随时互相挑战难题。爱丽丝是三个人中最聪明的。她会在纸上画一个数独棋盘,并填入一些约束条件。然后,她会让鲍勃和查理尝试解决这个难题。
证明 #
有一天,鲍勃出了一道非常难的数独题,爱丽丝花了很长时间尝试去解开这个数独,但是怎么都解不出结果。爱丽丝觉得鲍勃在耍她,“这题压根就无解!鲍勃你耍我!”,她跑到鲍勃那抱怨。
“呵呵,我能证明给你看这题是有解的,而且我知道这个解“,鲍勃淡定的回答道。
“好啊“,爱丽丝暗自想着,“哼哼,等你证明给我看之后,我就把解记下来然后去戏耍一下查理,给他也做一下这题。”
鲍勃接着说:“我会用零知识证明的方法给你证明我会这题的解。也就是说我不会把解给你看,却能让你信服我确实有这题的解。”
爱丽丝并不相信他能这样做到,还在想象查理被耍的样子。
承诺 #
鲍勃拿出81(9x9)张空白的卡片放在桌上,在每张纸上写上1-9中的一个数字,他让爱丽丝转过身闭上眼,然后把这81张卡片小心翼翼地按照解的排列放在桌上,代表谜底的卡片,数字面朝下放在桌上;代表谜面的卡片,则数字面朝上放在桌上。

随机挑战 #
鲍勃放好卡片后,让爱丽丝睁开眼转过身。爱丽丝很激动,她觉得谜底就要揭晓了,很是开心。她可花了好几天时间都没能解出这题。
鲍勃对爱丽丝说:“爱丽丝,你不能偷看这些面朝下的卡片。“,明显能看出爱丽丝很失望,她以为能看到完整的一个解。“但是我能让你检验这些解:你可以随意选择按照行(row),或者按照列(column),或者按照3x3的九宫格(box) 来检验我的解。你挑一种吧~”
验证 #
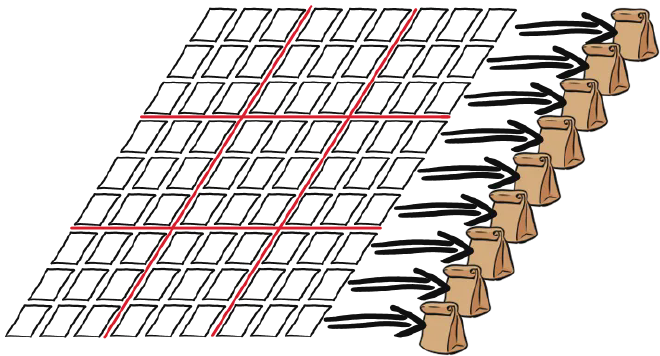
“好了,你可以打开这些布袋了。“鲍勃对爱丽丝说,“每个布袋里应该都有正好9张,没有重复数字的,分别是数字1-9的卡片。” 爱丽丝打开每个布袋一看,还果真是这样。

“可这啥都证明不了啊!我也可以这样做给你看。我只要保证每一行都是1-9这9张卡片,不去管纵列和九宫格里的数字是不是也都是没有重复的不就行了。“爱丽丝气急败坏的说道。
鲍勃解释说:“可是我事先也不知道你会选按照行来收集卡片,还是按照列,还是按照九宫格啊。我又不是你肚子里的蛔虫。。。我是按照题解来放置卡片的,你选啥我都没在怕的”
爱丽丝想了想,确实,一个数独只有真正正确的解才能保证每一行每一列每一个九宫格里的数字都是没有重复的1-9。鲍勃如果真的在骗她,鲍勃不会那么理直气壮,爱丽丝也至少有1/3的概率可以抓到他在骗人。
重复 #
爱丽丝还是不服气。觉得鲍勃仍然有可能在骗她,所以要求鲍勃再把卡片复原,按照原来的方法,重新选。这样接连试了几次,爱丽丝每次都选一个不一样的试验方法。试了好多次都是一样的结果。爱丽丝这下不得不承认,鲍勃要么运气非常非常好,每次都能押中爱丽丝会选择哪种试验方式,要么就是他确实知道题解,(或者鲍勃会读心术能预先知道爱丽丝会选什么试验方式)。爱丽丝很失望,这么多次试验下来,她还是不知道真正的题解,她只知道每次鲍勃放置卡片的排列里很大几率每行每列每个九宫格确实都是没有重复的1-9,这就说明很大几率这题是有解的,而且鲍勃很大几率确实知道这题的解。
鲍勃把这种零知识证明的方法也给查理展示了一遍。从此之后三个好友养成了通过零知识证明去证明给对方看自己知道某题解的习惯。毕竟每个人在解题的时候都花了很大功夫,不想轻易地把题解直接告诉对方。虽然每次零知识证明的过程很花时间,但是他们都乐在其中。
区块链和全球数独革命 #
有一天,爱丽丝想到了一个好主意。知道她对数独的热爱在网上有数百万人分享,她决定开设自己的 YouTube 频道,在那里她可以在线发布自己的数独挑战。她称其为“数独区块链”(她不知道区块链到底是什么,但这是一个非常酷的流行语)。她梦想着许多频道订阅者会向她发送比特币,并决定加入竞争的数独频道所没有的功能:她要求鲍勃使用零知识证明来验证每个谜题的解决方案是否存在。她会把整个事情拍下来,放在数独区块链上,这样每个人都会知道(很有可能)每个谜题都是可以解决的。
作弊 #
有一天,爱丽丝来到鲍勃家记录数独挑战的证明,却发现她把谜题的答案留在了家里。由于她急于在网上发布新的挑战,她恳求鲍勃无论如何都要和她一起拍摄。她说服鲍勃假装和她一起做证据。他们一起商定了一系列测试(行/列/和块),鲍勃 将“随机”选择这些测试。由于爱丽丝也知道测试的顺序,她可以很容易地通过它们,而没有谜题的答案。
查理在国外旅行并看到了这段视频,后来当爱丽丝和鲍勃告诉他他们是如何拍摄的时,他感到惊讶。“我再也不会相信你们两个了!”他大声说。“没有人应该相信你的任何在线视频证明!”
不可思议的机器和非交互式证明(Non-interactive Proofs) #
查理很沮丧。他不想轻易放弃自己的数独解谜习惯,但知道爱丽丝和鲍勃不值得信任,他想要一种远程检查证明的方法。经过几个不眠之夜,他向爱丽丝和鲍勃宣布他有了一个新主意。他把自己锁在房间里几个小时,整夜疯狂地工作。早上,查理向爱丽丝和鲍勃展示了他令人难以置信的新发明:零知识数独非交互式证明机(“The Zero-Knowledge Sudoku Non-Interactive Proof Machine” or zk-SNIPM)
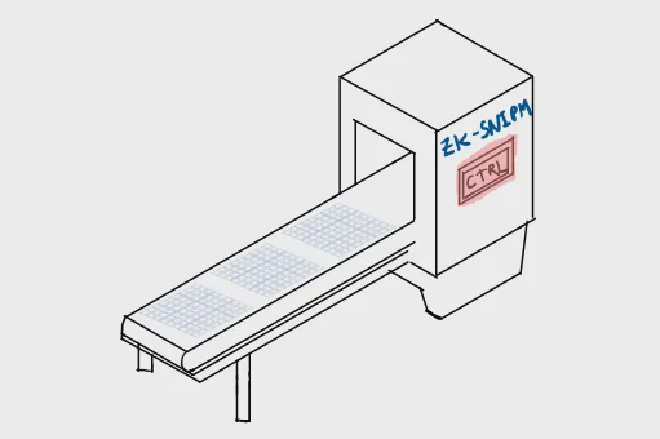
这台机器基本上就是把鲍勃和爱丽丝之前当面做的那套证明自动化,不再需要人为交互。鲍勃只要把卡片放在传送带上,机器会自动选择按行,或列,或九宫格来收取卡片,放到袋子里打乱顺序,然后把袋子通过传送带再送出来。然后鲍勃就可以当着镜头的面拆开袋子展示里面的卡片。
这台机器有一个控制面板,打开里面是一串旋钮,这些旋钮用来指示每次试验的选择(行,列, 九宫格)。
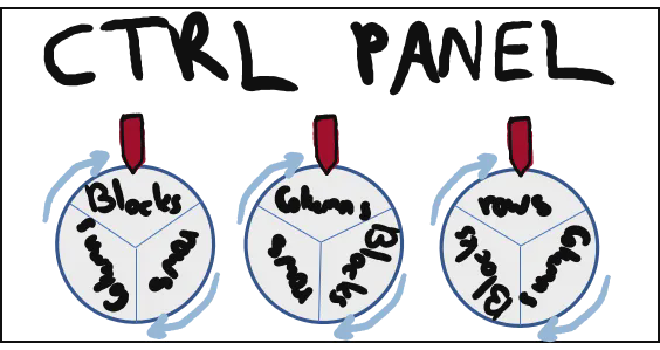
查理已经设置好了试验的序列,然后把控制面板焊死,以保证鲍勃和爱丽丝不会知道他到底选择了怎么样一个试验序列。
这下查理很放心,他可以完全信任自己这台机器,放心的把机器交给鲍勃和爱丽丝,让他俩下次直播就直接用这台机器来证明。查理相信有了这台机器他俩就没法再开挂了。
仪式 #
鲍勃和爱丽丝很嫉妒查理的这台机器,并且想也能用这台机器来验证查理自己出的数独题。但是问题是,查理是知道自己选了什么样的试验序列的,如果用同一台机器去验证查理自己的数独题解,查理就可以开挂。鲍勃把大伙聚集起来提议让查理把控制面板重新打开,然后大家一起来设置控制面板上的试验序列。鲍勃把这个过程称为“可信任的初始设置仪式(trusted setup ceremony)”。
鲍勃提议把这台机器放在一个漆黑的屋子里,把旋钮上的指示贴纸都撕去。他们三人分别进入这个屋子,爱丽丝还提议大家进房间时蒙上眼来保证随机性,并且带一顶锡纸做的金属帽子(爱丽丝还是怀疑鲍勃多少会一点读心术,想通过锡纸帽子来屏蔽脑电波信号防止读心术(side-channel attack))。这样,最后这些旋钮所代表的试验序列他们三个人都没有办法知道。就算他们3人中有2人事先商量好自己会怎么选,他们也无法得知第三个人会怎么选,从而没有办法作假。这个仪式结束之后,他们一起把控制面板焊死。
破解这台机器 #
一天下午,爱丽丝和查理出去玩儿了。鲍勃一个人在家守着这台机器。他开始琢磨它是不是像查理说的那样安全可靠。过了一会,他开始给机器故意传送一些假的题解(只保证每行或每列或每九宫格的数字不重复),试图通过这种试错来找出机器里设置的试验序列。慢慢的,鲍勃把机器里的试验序列都推断出来了。他既兴奋又沮丧,你能帮鲍勃设计一个更好的证明机吗?
故事的本质 #
故事讲完了,相信大家对零知识证明有了一个大概的印象。零知识证明的本质就是在不揭晓我所知道或拥有的某样东西的前提下,向别人证明我有很大几率(这点很重要,零知识证明说到底是一个概率上的证明)确实知道或拥有这个东西。
故事里要证明的东西就是一个数独题的解,鲍勃让爱丽丝每次随机抽取行,列,九宫格的卡片,并收集在一起随机打乱,爱丽丝通过拆开袋子并不能知道题解,但是却能相信鲍勃很大几率确实知道题解。
这个故事里的zk-SNIPM也是半开玩笑地暗指了零知识证明现在最普遍的zk-SNARKs(Zero-Knowledge Succinct Non-Interactive Argument of Knowledge)算法。故事中的zk-SNIPM虽然存在漏洞,但是他还有改进的余地,比如用一台扫描仪把第一次卡片的组合就全扫描下来,然后一次性同时验证所有的试验序列。这样就很难通过试错的方式来破解机器。
鲍勃和爱丽丝之间最开始那种互动式的证明方法暗指的是交互式零知识证明(interactive zero-knowledge proof)。交互式零知识证明需要验证方(爱丽丝)在证明方(鲍勃)放好答案(commitment)后,不断的发送随机试验。如果验证和证明双方事先串通好,那么他们就可以在不知道真实答案的情况下开挂(simulate/forge a proof)。
非交互式的证明则不需要这种互动。但是会额外需要一些机器或者程序,并且需要一串试验序列,这个试验序列不能被任何人知道。有了这么一个程序和试验序列,证明机就能自动算出一个证明,并且能防止任何一方作假。
主打匿名性的区块链加密货币ZCash里用到了零知识证明来保证交易双方和交易金额的匿名性。ZCash团队举行过2次故事中的那种仪式,第一次仪式他们甚至拍摄了一个纪录片,第二次仪式中一组人甚至不惜代价去切尔诺贝利核事故发生地取来了带有核辐射的废料,然后在高空中用利用核辐射来生成随机数。 有兴趣的各位可以去看看ZCash仪式的相关资料,非常有趣。
